统计学是一门研究数据的科学，通过如何有效地收集、整理和分析这些数据，探索数据内在的数量规律性，对所观察的现象做出推断或预测，最终为采取决策提供依据。

▋ 统计学在体外诊断试剂研发、注册、使用等各阶段的应用

在体外诊断试剂研发、注册、生产、临床使用等各个过程中都会涉及到统计学知识的应用，我总结如下：

各应用方面及常用统计方法

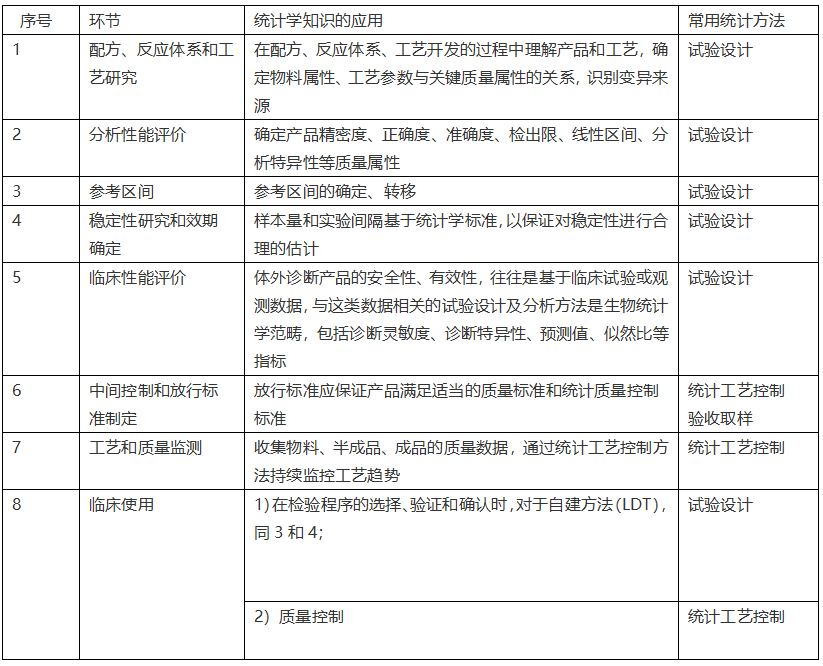
▍如何正确应用统计学

统计学很重要，是一个有用的工具，它能帮助我们理解、梳理外部世界中的庞大信息，滤掉一些无用信息，抽取有用信息，同时处理存在不确定性的数据。但是，对于我们体外诊断和医学检验的从业者来说，统计学相关知识和应用一直是我们的难点和障碍。这里我举医学实验室测量不确定度评定的国际标准起草过程来说明。ISO/TC 212曾经制定过一个标准ISO 25680《Medical laboratories — Calculation and expression of measurement uncertainty》，该标准是采用经典的自下而上的方法对不确定度进行评定，比较繁琐，对常规实验室而言难度太大，另外针对医学实验室特殊性不强，缺乏实用性，最终该标准2009年投票未通过。后来ISO/TC 212又重新启动制定，制定的时候明确要制定出 “a  simple ‘how to do’ document aimed at routine  lab staff lacking in knowledge of metrology and statistical competence，Using lab language , e.g. SD, CV”，因此看来统计学知识不足是我们这个行业普遍的特点，不分国界。

统计学不是万能的。统计学有所为，有所不为，我们学习统计学就要理解这当中的差异。举一个实例，有同仁在IVD试剂稳定性评价的时候，采用t检验，发现试剂精密度不好，怎么都合格。试剂精密度越好，越吃亏，下降1%~3%都不行。这是一个非常现实的问题，因此要正确理解统计学。总之，学习统计学一定要结合学科和研究的需要，这样才是真正学懂了统计学。摘别人的一段话“统计是一门解决不确定问题的方法和策略，凡是确定性的问题，拿统计去解释完全是自扰，凡是不可能事件，统计学上连给出一个零都不成”。

▍统计学的一些基本概念

下图说明了统计学研究的目的和过程。

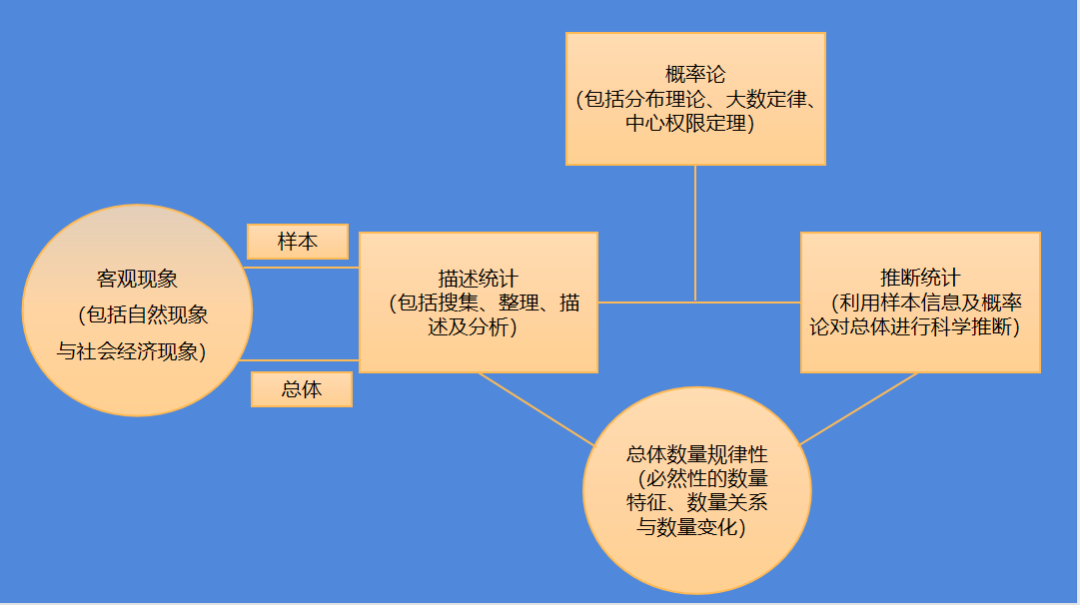
有两种常用的统计方法：描述统计和推断统计。尽管描述统计很有用，但是它只能提供基本信息，因此我们最关注的是推断统计，推断统计是研究如何根据样本数据去推断总体数量特征的方法，它是在对样本数据进行描述的基础上，对统计总体的未知数量特征做出以概率形式表述的推断。推断统计又有2种方法，即参数估计和假设检验。参数估计是由对部分进行观测取得的数据对研究对象整体的数量特征取值给出估计的方法。假设检验是由对部分进行观测取得的数据对研究对象的数量规律性是否具有某种指定特征进行检验。下图是推断统计的过程。

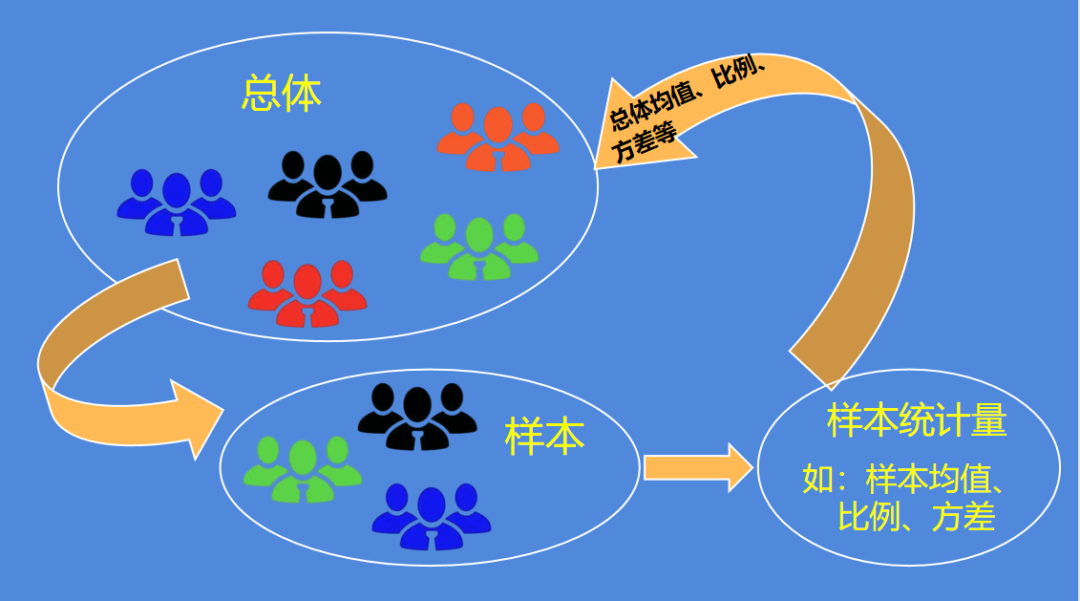
我们要理解统计学的一些基本概念，特别是以下的几个术语：

• 总体（population）：根据研究目的确定的同质研究对象的全体（集合）。

• 样本（sample）：从总体中随机抽取的部分观察单位。

• 变量（variable）：总体中个体单位所具有的特征或特性。

• 随机变量：某次试验结果的数值性描述。

• 离散型随机变量：只能取有限个或可数个数数值的随机变量。

• 连续型随机变量：可以取一个或多个区间中任何值的随机变量。为便于理解，将随机变量的取值设想为数轴上的点，每一个试验结果对应一个点。如果一个随机变量仅限于取数轴上有限个或可列个孤立的点，离散型；如果一个随机变量是在数值上一个或多个区间取任何值，连续型。

• 参数：用来描述总体的数量特征的，见下表

• 统计量：是用来描述样本的数量特征的，见下表

▍抽样及抽样方法

因为是用样本去估计总体，必然涉及到抽样，抽样的目的是用样本的统计量（均值、标准差、方差等）去估计总体参数（均值、标准差、方差）。抽样及抽样方法直接关系到数据质量。抽样方法有简单随机抽样（又分为直接抽选法、抽签法、随机数表法等）、分层抽样（先分层）、系统抽样（先排序，一般针对样本量大的情况）、整群抽样（先分群）等几种方法，其中最常用的是简单随机抽样，在这里一定要注意的是：随机抽样不等于随便抽样、随意抽样。

抽样也会带来抽样误差，抽样误差是指利用样本推断总体时产生的误差，抽样误差不能避免的，由于样本只是总体的一部分，用样本的信息去推断总体，或多或少总会存在误差。但是抽样误差可以计算和控制的。如果是随机抽样，则样本容量越大，抽样误差越小，抽样误差与样本容量的平方根呈反比，这里就要涉及到样本容量的确定。理论上，样本容量越大越接近总体越好，但事实上，样本量=精度+费用，它是精度和费用的函数，确定样本容量，需要处理好设定的精度与现有经费，同时也要考虑资源、时间等限制条件，最终的样本量确定是在上述因素之间的权衡关系。

从一个假定的小总体中进行抽样，并观察所有可能的样本均值形成的抽样分布，随着样本量n的增加，n足够大（通常≥30），发现无论总体分布如何，样本均值形成的分布越来越趋于正态，样本均值的均值就等于总体均值，样本均值的方差等于总体方差除以样本量n。这就是中心极限定理的应用，中心极限定理告诉我们，当样本足够大时，样本均值的分布会慢慢变成正态分布。中心极限定理指的是给定一个任意分布的总体，每次从这些总体中随机抽取 n 个抽样，一共抽 m 次。然后把这 m 组抽样分别求出平均值， 这些平均值的分布接近正态分布。

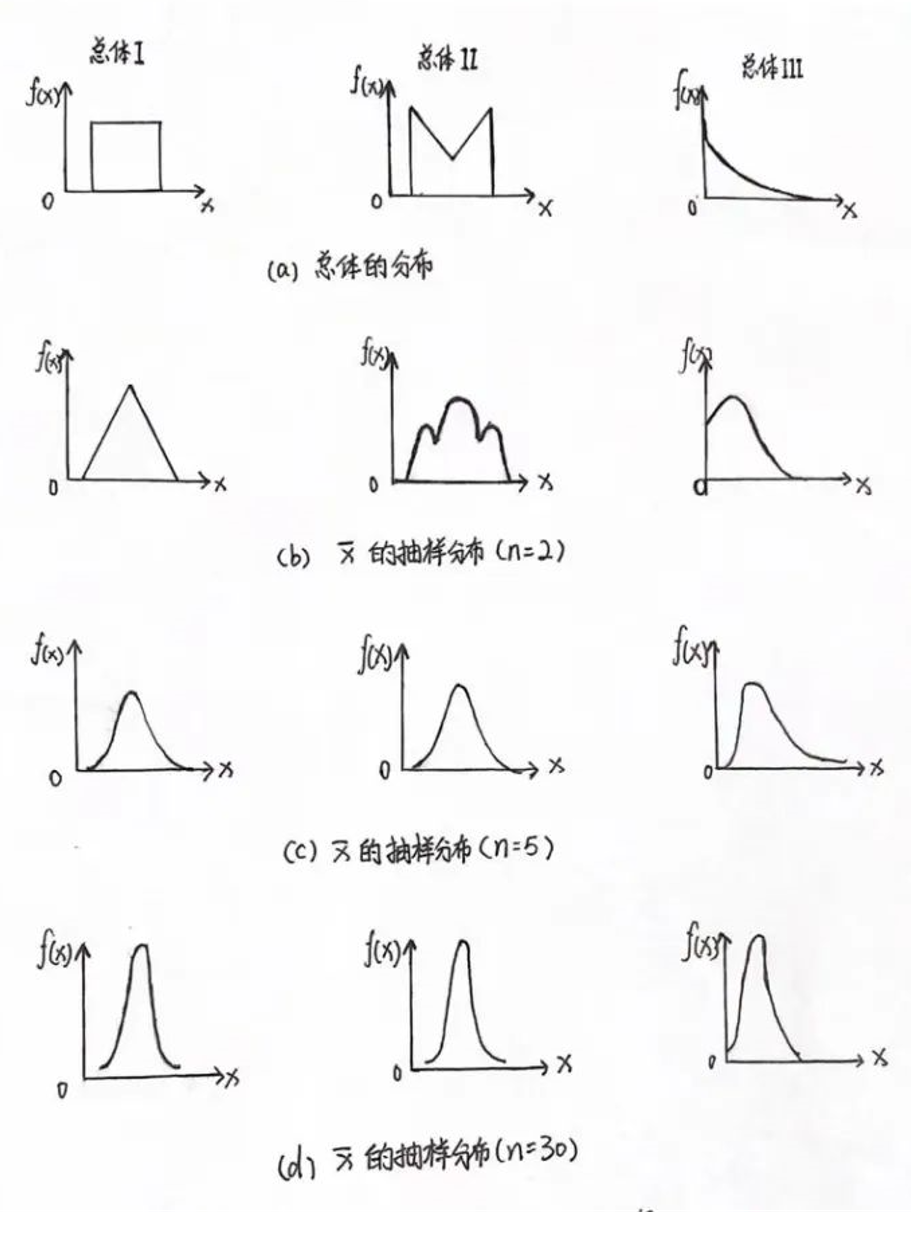
再进一步总结，对于总体分布是正态分布，其大样本、小样本均为正态分布。对于非正态分布，大样本呈正态分布，小样本呈非正态分布。

对于抽样方法和样本量，举例看看JJG 1006-94《一级标准物质技术规范》的规定，需要对标准物质的均匀性进行抽样检验。文件里面这样规定：

抽取单元数：抽取单元数目对样品总体要有足够的代表性。抽取单元数取决于总体样品的单元数和对样品的均匀程度的了解。当总体样品的单元数较多时，抽取单元数也应相应增多。当已知总体样品均匀性良好时，抽取单元数可适当减少。抽取单元数以及每个样品的重复测量次数还应适合所采用的统计检验要求。 当总体单元数少于500时，抽取单元数不少于15个，当总体单元数大于500时，抽取单元数不少于25个。 对于均匀性好的样品，当总体单元数少于500时，抽取单元数不少于10个；当总体单元数大于500时，抽取单元数不少于15个。

取样方式： 在均匀性检验的取样时，应从待定特性量值可能出现差异的部位抽取，取样点的分布对于总体样品应有足够的代表性，例如对份状物质应在不同部位取样；对圆棒状材料可在两端和棒长的1/4、1/2、3/4部位取样，在同一断面可沿直径取样。对溶液可在分装的初始，中间和终结阶段取样。

在ISO导则35《标准物质/标准样品定值的 一般原则和统计方法》中是这么规定样本量：

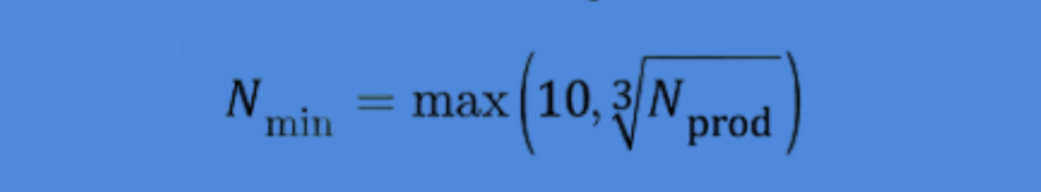
目前，在我们实际工作中，抽样工作容易被忽视。随便抽样、随意抽样、样本量n的确定无根据等现象还是比较常见的。希望通过抽样的介绍，大家能进一步重视抽样工作。