谁来代表我们?—统计学在体外诊断中的应用(三)
2022-05-23 08:54:05来源 | 网络
上一篇提到要关注离群值,离群值代表了数据的质量,对检出的统计离群值,应尽可能寻找其技术上和物理上的原因,应根据实际问题的性质,权衡寻找和判定产生离群值的原因所需代价、正确判定离群值的得益以及错误剔除正常观测值的风险,作为处理离群值的依据。
在进行完数据检查后,我们要对数据进行分析和描述,重点关注三个指标:
① 反映分布集中趋势的指标;
② 反映分布离散程度的指标;
③ 反映分布形状的指标。
【本篇我们重点介绍反映分布集中趋势的指标】
数据分布集中趋势的指标反映的是数据一般水平的代表值,或者数据分布的中心值,或者是数据的平均指标。从不同角度考虑,集中趋势的指标有多个,下面我对常用的、代表性的指标加以介绍。
(一)众数
众数(mode)是将数据按大小顺序排队形成次数分配后,在统计分布中具有明显集中趋势点的数值,是数据一般水平代表性的一种。正态分布和一般的偏态分布中,分布最高峰所对应的数值即众数。如果没有明显的集中趋势或最高峰点,众数可以不存在。当然,如果有两个高峰点或集中趋势,也可以有两个众数。如下图所示:
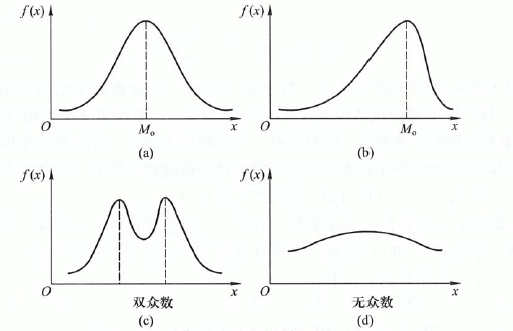
图1 众数示意图
简单说,众数就是一组数据中出现次数最多的数值。
例:
1,2,3,3,4 的众数是3
1,2,2,3,3,4 的众数是2和3
1,2,3,4,5 没有众数
(2)中位数
数据排序后,位置在最中间的数就是中位数(median)。显然,中位数将数据分成两半,一般数据比中位数大,一半数据比中位数小。 例: 1,2,3,3,4 的中位数是3 1,2,2,3,3,4 的中位数是2.5 1,2,3,4,5 的中位数是3
如果数据个数为偶数,例如1,2,2,3,3,4,则中位数位置=(6+1)/2=3.5,即在第三个数值2和第四个数值3之间,显然中位数是2.5。我们看到中位数是从位置上确定得,个别极端大值或极端小值的变化不影响中位数数值,因此中位数具有稳健性。例如,本例中6个数据的最大值4变为14,即1,2,2,3,3,14,此时中位数仍然是2.5。 需要注意的是若数据大量重复某一数值,这时的中位数未必准确。举例:某地抽出100户,经调查发现,20户是两口之家,40户是三口之家,40户是四口之家, 中位数是3,但不能说有一半家庭规模比三口人多,一半家庭比三口人少。 另外,中位数有这样一个性质,就是数据值与中位数之差的绝对值之和最小,即:
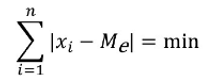
(03)分位数
中位数是将统计分布从中间分成面积(即数据个数)相等的两部分,与中位数性质相似的还有四分位数(quartile)、十分位数(decile)和百分位数(percentile)。显然,四分位数就是将数据分布4等分的三个数值,其中中间的四分位数就是中位数。十分位数和百分位数就是将数据分布10等分和100等分的数值。
这里举个网络上摘抄过来的例子:村里有1000位村民,有高有矮,最矮的1.5米,最高的1.9米,可以把这些人按照高矮排成一排。经过计数,发现1%的人低于1.52米,这样1.52就是第1个百分位;再数数,95%的人身高低于1.81米,那么1.81就是第95个百分位;继续数,只有10个人即1%超过1.89米,于是1.89就是第99个百分位。 在这里特别提一下心肌梗死定义专家共识中,明确把心肌肌钙蛋白检测作为诊断心肌梗死(MI)的首选心肌标志物诊断指标,并以第99百分位数的健康人群的cTn及其动态变化作为主要判断标准。第99百分位的意思就是99%的健康人低于此值,只有1%的人超过此值。国际临床化学联合会(IFCC)最新文件要求样本量不能低于600(男女各半),这样第99百分位cTn值才能准确。
(04)均值
均值(mean)就是算术平均值,是数据集中趋势的最主要、最常用的一个指标,计算公式如下:
简单均值: 加权均值: 均值是一组数据的均衡点所在,是一组数据的误差相互抵消后的客观事物必然性数量特征的一种反映。均值有一些重要的数学性质,数据观察值与均值的离差之和为零,数据观察值与均值的离差平方和最小。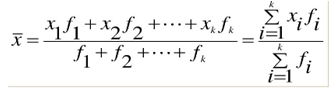
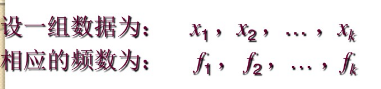
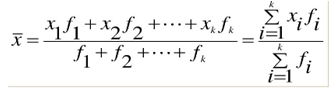
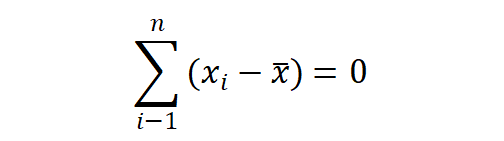
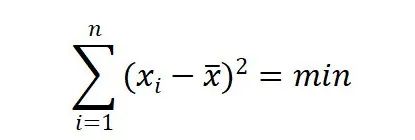
(05)几何平均数
几何平均数:(geometric mean)在计算方法上可以看作是算术平均数公式的变形。计算公式如下:
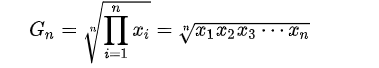
几何平均数平均的不是实际数据,而是一些比率值,几何平均数在计算社会经济问题的平均发展速度等方面有很重要的作用,举一个例子:
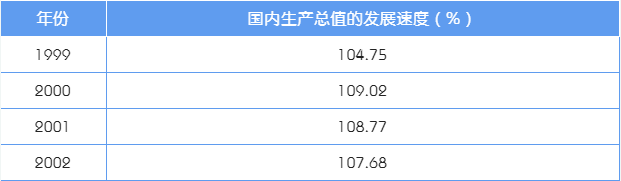
表1 1998-2002年我国的国内生产总值的发展速度
求平均发展速度:
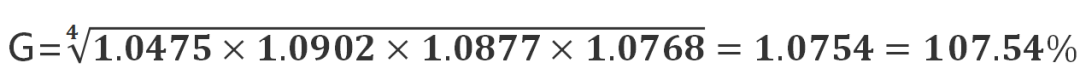
此处不能计算算术平均数,因为这4个发展速度分别是在前一年生产总值增长的基础上进一步增长的,也就是说每一年变化的分母是不同的,应该用几何平均数。
(06)切尾均值
切尾均值(trimmed mean)是去掉大小两端的若干数值后计算中间数据的均值,常常用在一些体育比赛中。这里不详细介绍。
最后,我们再来进行小结。本篇中介绍了众数、中位数、均值、几何平均数和切尾均值这5种表示数据一般水平的代表值,其中我们要重点关注众数、中位数、均值。
众数、中位数是从数据分布形状及位置角度来考虑的集中趋势代表值,而均值是经过对所有数据计算后得到的集中趋势值。显然,这三个代表值的不同特点决定了实际应用中要根据不同的研究目的和不同的数据特征来选择适当的代表值。
Ø 在对称分布中,众数、中位数、均值都是同一数值,见图2。
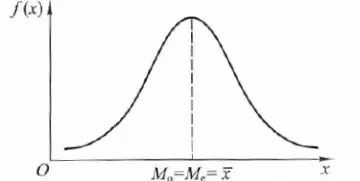
图2正态分布的众数、平均数、中位数
Ø 但在偏态分布,众数、中位数、均值就不再是同一数值了。当数据呈现偏态分布时,众数、中位数、均值就不再相同或相似,偏斜程度越大,三个数值间差别越大。见图3。
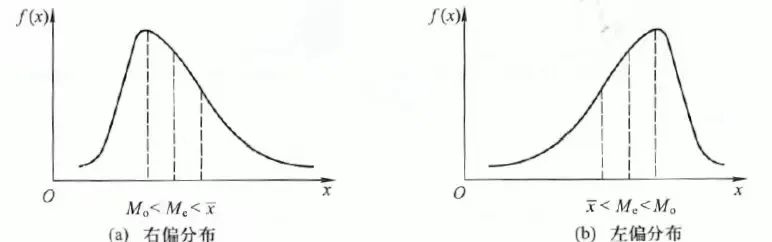
图3偏态分布的众数、平均数、中位数
为了加深印象,我们再举一个例子出自CLSI EP09c Measurement Procedure Comparison and Bias Estimation Using Patient Samples。
图4:方法间偏差基本恒定,但是随着浓度不同,偏差呈正态分布,所以最终偏差取了平均值。
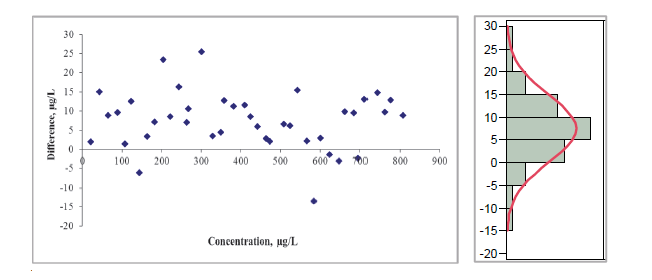
图4 方法间偏差呈正态分布
图5:方法间偏差基本恒定,但是随着浓度不同,偏差呈偏态分布,所以最终偏差取了中位数。
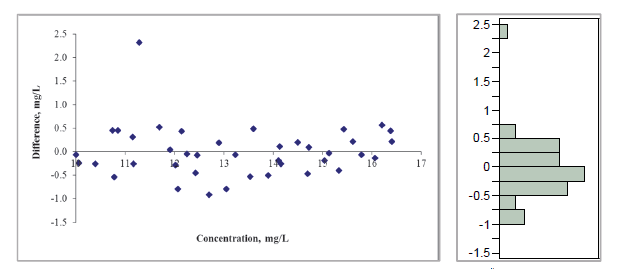
图5 方法间偏差呈偏态分布
【注意啦】
敲黑板!
今日分享再给大家做个最简短的归纳总结!
◢ 众数、中位数、均值、几何平均数和切尾均值这5种数据分布集中趋势的指标,反映的是数据一般水平的代表值,或者数据分布的中心值,或者是数据的平均指标;
◢ 中位数很容易理解、很直观,不受极端值影响,特别适用于偏态分布;
◢ 均值是对所有数据平均后计算的一般水平代表值,数据信息提取得最充分,特别适用于用样本信息推断总体信息。
【上期干货】
认识统计学对体外诊断的重要性—统计学在体外诊断中的应用(一)