工科直男的选择—关注数据离散程度 统计学在体外诊断试剂中的应用(四)
2022-06-20 13:39:11来源 | 网络
工科直男的选择—关注数据离散程度
上一篇我们关注反映分布集中趋势的指标,集中趋势表示的是分布的中心位置或一般水平的代表值。我们不能仅仅关注代表值、平均值、中心值,我们也要关注差异程度。
☉ 举一个栗子,某工科直男找工作,有三份工作机会摆在他面前,三份工作的月平均收入分别是10k、15k、30k。从平均值来看,不容置疑第三份工作好。但工科男学过统计学,他又仔细算了一笔账。第一份工作是在国企,工资雷打不动,每个月都是10k。第二份工作是在私企,工资每月在10k~20k浮动,因为有“万恶的KPI”。第三份工作,有个创业小机会摆在他面前,收入剧增,但是收益与风险并存,干得好的时候一个月60k也有可能,订单没有时就得吃馒头咸菜。
从这个栗子反映出了收入有浮动,怎么测算收入的浮动程度呢?本篇介绍几个常用的、代表性的指标。
◢ 1. 极差
极差(range)也称为全距,是数据最大值减去最小值之差,它是数据离散或差异程度的最简单测度值,即R=max(xi)-min(xi)。显然,数据的分散程度越大,极差就越大。极差的计算很简单,但它易受极端值的影响,因为它只利用了数据两端的信息。
◢ 2. 内距
内距(inter-quartile range, IQR)是两个四分位数之差,即内距=上四分位数-下四分位数=Q3-Q1。内距是与集中趋势代表值中四分位数相对应的离散程度代表值。内距基本不受极端值的影响,而且内距反映的是中间50%数值大小的差异,显示比极差更多的数据差异信息。
◢ 3. 方差和标准差
方差(variance)是离差平方的平均数,即
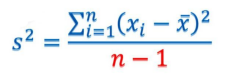
这是样本方差的计算公式,s2表示样本方差,


标准差是方差的平方根,即
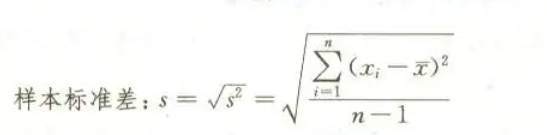
方差是以平方的形式,使得有正有负的离差变成正的了,由于平方,改变了离差的单位,因此就有必要开平方根而得到与原单位相同的单位。
◢ 4. 变异系数
变异系数(又称离散系数,Coefficient of Variation,CV),当需要比较两组数据离散程度大小的时候,如果两组数据的测量尺度相差太大,或者数据量纲的不同,直接使用标准差来进行比较不合适,此时就应当消除测量尺度和量纲的影响,而变异系数可以做到这一点,它是标准差与平均值的比。CV没有量纲,这样就可以进行客观比较了。变异系数计算公式 CV =( 标准差 s / 平均值 
以上各个都是反映零散程度的指标,日常工作中,我们用得最多的是极差、标准差(或变异系数),那什么时候用极差,什么时候用标准差呢?查阅体外诊断试剂行业标准,对于试剂的批内精密度(重复性)验证,都是采用标准差(或变异系数)这个指标,但是对于批(号)间差,有的标准采用极差,有的标准采用标准差(或变异系数)。例如这个标准:

再例如这个标准:

我们以一组数据举例来说明两种方法间的差异,例如批号1的3个测试数据:110,115,114,批号2的3个测试数据:101,105,107,批号3的3个测试数据:116,118,120。按照第一种方法计算,极差=14,相对极差R=12%,按照第二种方法计算,标准差=6.4,变异系数CV=6%。两种方法算出来,极差与标准差差别较大,因此相对极差与变异系数差别也很大。相对极差12%反映试剂批号间差异比较大,但是看变异系数CV 6%似乎批间差可以接受,从3批的数据看,试剂批号间差异还是存在的,相对极差12%更接近真实的情况,因为标准差(或变异系数)是以均值为中心计算出来的,在一定程度上抵消了数据大小不等的影响。
最后,一句话总结:数据集中程度和数据离散程度,都是对数据的描述和分析,他们是一对既对立又统一的指标。再回到开头的栗子,假如你是工科男,你会选择哪份工作?
往期回顾:
认识统计学对体外诊断的重要性—统计学在体外诊断中的应用(一)