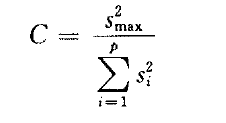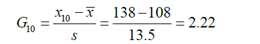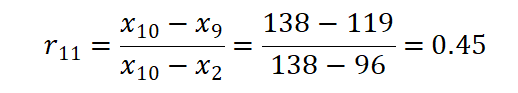寻找“离群值”—统计学在体外诊断中的应用(二)
2022-05-13 18:51:35source | 网络
上一篇提到抽样,例如体外诊断试剂研发流程中的关键一步——中试阶段,在GMP条件下生产出3批产品,进行产品分析性能评价、临床性能评价、稳定性研究、参考区间或阳性判断值确定、注册检验等工作,这里面就涉及到抽样,从生产出的产品中随机抽取出一定数量,做实验,获得一系列数据,通过对这些数据进行分析处理,最后获得产品的特征参数。
【这一篇我们重点关注数据离群值的判断和处理。】
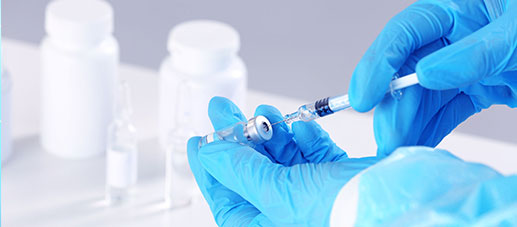
实验获得的数据,我们不能不管三七二十一,直接上来就计算均值、标准差、偏差。大多数的统计量,如均值、标准差、相关系数等,以及基于这些统计量的分析,均对离群值高度敏感。关注离群值,就是关注数据质量。如图1所示,左边是不去离群值的回归分析,右边是去掉离群值后的回归分析,可以看出回归线差别巨大。如果统计学上认为应该舍弃的数据留用了,势必会降低后续分析的可靠性。相反,本应该留用的数据被舍弃,虽然精密度提高,但却夸大了分析结果的可靠性,从而增加风险。
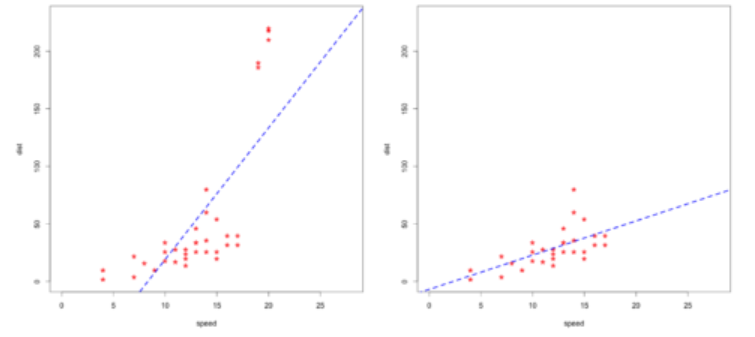
图1 离群值剔除和不剔除情况下的回归线
⑴ 什么是离群值
在一组平行测定中,若有个别数据离开其他数据较远,则把此数据视为可疑,即离群值(outlier)。
离群值出现会有两种情形,一种出现在数据的单侧,即都为“鹤立鸡群”的高值,或都为“拖后腿”的低值;第二种是出现在双侧,两边都有“不合群”的,即既有高值,也有低值。
离群值产生有两种来源,一是技术错误造成的,即样品错误、测试时的操作错误、仪器故障、计算错误、录入测试结果时的简单书写错误等造成的,这样的离群值可以直接剔除,或剔除后再做实验补数据;第二种来源是不能用技术错误解释的,产生于试验条件、试验方法等因素的偶然偏离,这时就要进行统计处理来决定离群值是保留还是剔除。离群值的取舍对分析结果会产生很大影响,必须谨慎对待,在离群值产生的原因不明之前,不应简单决定其取舍。
在做离群值检验时,要预先规定检出离群值个数的上限,若检出的离群值个数超过了这个上限时,对此样本应做慎重的研究和处理。
⑵ 离群值的几种常见检验方法
在统计学上检验离群值之前,建议先做散点图,这样通过散点图可以一目了然、直观地判断数据情况。如图二所示,离群点是孤立的一个或几个数据点,远离数据集中其他数据点。
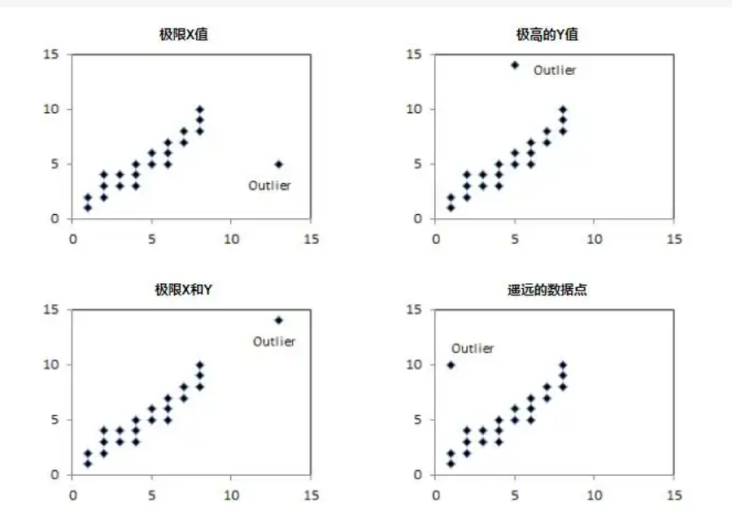
图2 绘制散点图
然后,我们再用统计学方法计算是否是离群值。本篇我们重点关注正态样本(事实上除去正态分布,还有重尾分布、偏态分布等类型,这些分布类型出现得较少,另外也比较复杂,因此我们可以不用重点关注)。设有一组正态样本的观测值,按其大小顺序排列为x1,x2,x3,……,xn。其中最小值 x1 或最大值 xn 为离群值 (xout)。对于离群值的统计检验,大都是建立在被检测的总体服从正态分布。基于此,在给定的检出水平α (通常取值为0.05) 或显著水平 α* (通常取值为0.01) 和样本容量 n 条件下,可查表获得临界值,再通过计算统计量后与临界值比较,若统计量大于临界值就判为异常。临界值表通常给出的是置信度 P,对双侧检验而言,P = 1 − α/2;对单侧检验而言,P = 1 − α。
(一)标准差已知情况
采用奈尔(Nair)检验法(样本量3 ≤ n ≤ 100),根据下式计算统计量Rn。
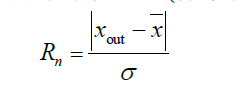
σ是已知的总体标准差。根据检出水平α 和样本容量查奈尔检验的临界值表值RP(n),若Rn > RP(n),判定为离群值,否则未发现离群值。
(二)标准差未知情况(限定离群值数量为1时)
更多情况下,数据的标准差是未知的,此时可采用的检验离群值的方法较多,本篇仅仅介绍常用的格拉布斯(Grubbs)检验法和狄克逊( Dixon )检验法。
1、 格拉布斯(Grubbs)检验法
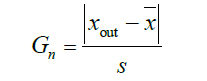

2、狄克逊( Dixon )检验法
此法由Dixon在1950 年提出,它的原理是通过离群值与临近值的差值与极差的比值,这一统计量rij 来判断是否存在离群值。由于样本容量大小的不同会影响此方法的准确度,因此根据样本容量的不同,统计量的计算公式不同,具体见下表。

判断离群值是最大值还是最小值,再根据样本容量n 代入对应的统计量计算公式,求出统计值 rij (或r 'ij)。确定检出水平α,查狄克逊检验的临界值表值 DP(n)。当 rij 或r 'ij > DP(n),判定为离群值,否则未发现离群值。
3、 t 检验法
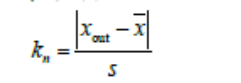

(三)标准差未知情况(离群值数量大于1 时)
当限定检出离群值的个数大于1时,可使用偏度-峰度检验法或狄克逊检验法的重复使用方法。
1、偏度-峰度检验法
偏度检验法适用于离群值出现在单侧的情形。
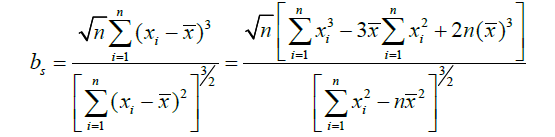
式中样本从小到大排列后的第 i 个数据称之为xi。确定检出水平α,查偏度检验的临界值表值bP(n),当bs > bP(n),判定为离群值,否则未发现离群值。当存在有多个离群值时,先选择最内侧的离群值进行检验。例如,当存在有两个上侧离群值 xn、xn−1,暂时去除 xn,测量次数减1,检验 xn−1 是否为离群值。若不为离群值,测量次数为n,再检测xn 是否为离群值。若xn−1 为离群值,xn自然也就舍弃了。
峰度检验法适用于双侧情形。确定检出水平 α,查峰度检验的临界值表值 P’b (n)。当 bk > P’b (n),判定离均值 最远的值为离群值,去除离群值后,重复峰度检验法检验是否仍然存在离群值,否则未发现离群值。
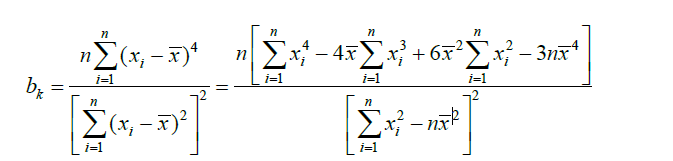
2、 格拉布斯(Grubbs)检验法 原理同上。 3、狄克逊( Dixon )检验法 原理同上。
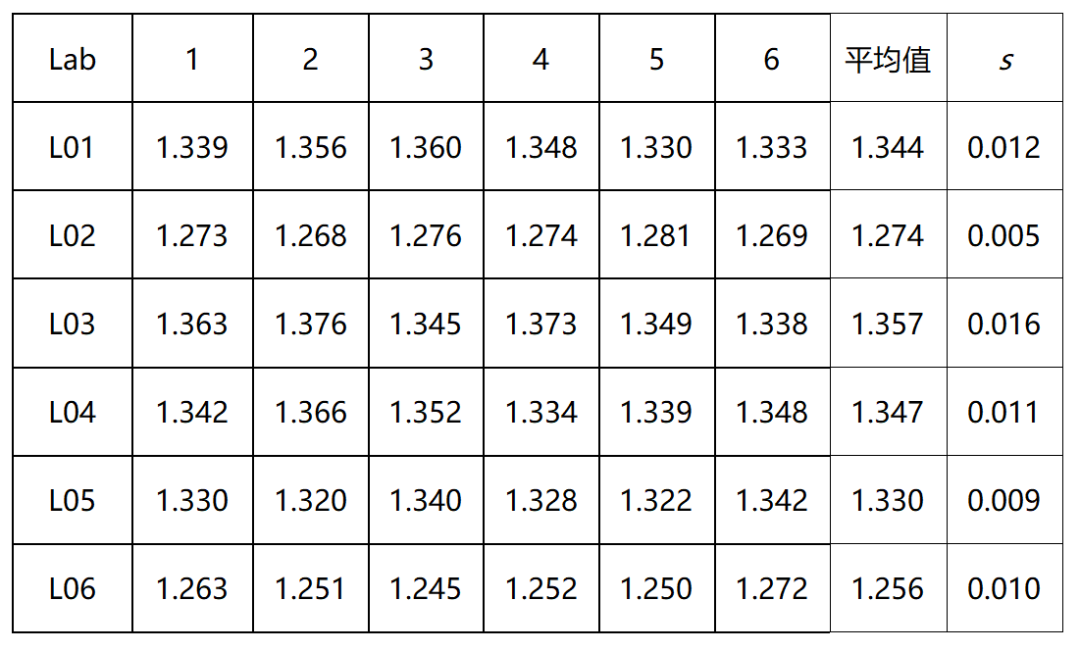
(四)组间数据等精度检验 以上的方法主要针对的是组内数据的检验。对于组间数据,可用柯克伦(Cochran)进行等精度检验,判断数据组间是否有显著性差异,然后再决定是否予以剔除。举一个例子,国家标准物质的定值有几种方法,其中一种方法是可由多个实验室合作定值。合作实验室的数目或独立定值组数应符合统计学的要求(当采用同一种方法时,独立定值组数一般不少于8个,当采用多种方法时,一般不少于6个)。当各个实验室的数据收集上来时,我们要对实验室间数据进行等精度检验。对于不等精度的数据,实验室根据具体情况进行剔除或采用不等精度加权方式处理。 给定p个由相同的n次重复测试结果计算的标准差si,柯克伦检验统计量C定义为 其中,smax是这组标准差中的最大值。如果C大于临界值,则视为统计离群值。 ⑶ 离群值检验的示例 例1: 对同一个样品进行10 次重复测试,将得到的数据按从小到大的顺序排列,91,96,99,101,104,108,111,114,119,138。检验是否存在上侧离群值。 已经检验出该数据服从正态分布。 方法一 格拉布斯法: 确定检出水平α = 0.05,查表得到G0.95(10) = 2.176,因为G10 > G0.95(10),所以判定138 为上侧的离群值。 方法二 狄克逊法 确定检出水平α = 0.05,查表得到D0.95(10) =0.477,因为 r11< D0.95(10),所以不能判定 138 为上侧的离群值。 不同的离群值检验方法可能会有不同的结果。本例中,狄克逊法通过极差比来判断是否存在离群值,当数据本身较为分散,极差比反映离群值的灵敏度就可能会下降,可能存在以假当真的情况。 例2: 6家实验室对Apo A-1候选标物进行协作定值,定值数据见表2。 表2 协作定值测量结果 单位:g/L 对测量结果进行等精度柯克伦(Cochran)检验,smax=0.016 查临界值表,C(0.05,6,6)=0.4184,C< C(0.05,6,6),表明各实验室间数据为等精度。 【上期干货】